Square root of -1

                                                      SQUARE ROOT OF  -1

Ramanujan Number

RAMANUJAN NUMBER

Five ways ancient India changed the world – with maths

INDIA changed the world with maths                                

 It should come as no surprise that the first recorded use of the number zero, recently discovered to be made as early as the 3rd or 4th century, happened in India. Mathematics on the Indian subcontinent has a rich history going back over 3,000 years and thrived for centuries before similar advances were made in Europe, with its influence meanwhile spreading to China and the Middle East.

As well as giving us the concept of zero, Indian mathematicians made seminal contributions to the study of trigonometry, algebra, arithmetic and negative numbers among other areas. Perhaps most significantly, the decimal system that we still employ worldwide today was first seen in India.

The number system

As far back as 1200 BC, mathematical knowledge was being written down as part of a large body of knowledge known as the Vedas. In these texts, numbers were commonly expressed as combinations of powers of ten. For example, 365 might be expressed as three hundreds (3x10²), six tens (6x10¹) and five units (5x10⁰), though each power of ten was represented with a name rather than a set of symbols. It is reasonable to believe that this representation using powers of ten played a crucial role in the development of the decimal-place value system in India.

Brahmi numerals. Wikimedia

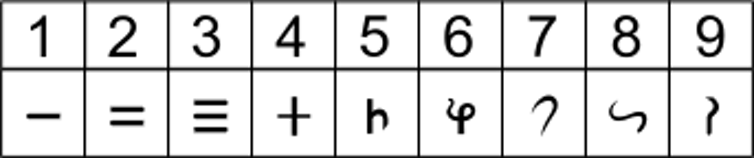
From the third century BC, we also have written evidence of the Brahmi numerals, the precursors to the modern, Indian or Hindu-Arabic numeral system that most of the world uses today. Once zero was introduced, almost all of the mathematical mechanics would be in place to enable ancient Indians to study higher mathematics.

The concept of zero

Zero itself has a much longer history. The recently dated first recorded zeros, in what is known as the Bakhshali manuscript, were simple placeholders – a tool to distinguish 100 from 10. Similar marks had already been seen in the Babylonian and Mayan cultures in the early centuries AD and arguably in Sumerian mathematics as early as 3000-2000 BC.

But only in India did the placeholder symbol for nothing progress to become a number in its own right. The advent of the concept of zero allowed numbers to be written efficiently and reliably. In turn, this allowed for effective record-keeping that meant important financial calculations could be checked retroactively, ensuring the honest actions of all involved. Zero was a significant step on the route to the democratisation of mathematics.

These accessible mechanical tools for working with mathematical concepts, in combination with a strong and open scholastic and scientific culture, meant that, by around 600AD, all the ingredients were in place for an explosion of mathematical discoveries in India. In comparison, these sorts of tools were not popularised in the West until the early 13th century, though Fibonnacci’s book liber abaci.

Solutions of quadratic equations

In the seventh century, the first written evidence of the rules for working with zero were formalised in the Brahmasputha Siddhanta. In his seminal text, the astronomer Brahmagupta introduced rules for solving quadratic equations (so beloved of secondary school mathematics students) and for computing square roots.

Rules for negative numbers

Brahmagupta also demonstrated rules for working with negative numbers. He referred to positive numbers as fortunes and negative numbers as debts. He wrote down rules that have been interpreted by translators as: “A fortune subtracted from zero is a debt,” and “a debt subtracted from zero is a fortune”.

This latter statement is the same as the rule we learn in school, that if you subtract a negative number, it is the same as adding a positive number. Brahmagupta also knew that “The product of a debt and a fortune is a debt” – a positive number multiplied by a negative is a negative.

For the large part, European mathematicians were reluctant to accept negative numbers as meaningful. Many took the view that negative numbers were absurd. They reasoned that numbers were developed for counting and questioned what you could count with negative numbers. Indian and Chinese mathematicians recognised early on that one answer to this question was debts.

For example, in a primitive farming context, if one farmer owes another farmer 7 cows, then effectively the first farmer has -7 cows. If the first farmer goes out to buy some animals to repay his debt, he has to buy 7 cows and give them to the second farmer in order to bring his cow tally back to 0. From then on, every cow he buys goes to his positive total.

Basis for calculus

This reluctance to adopt negative numbers, and indeed zero, held European mathematics back for many years. Gottfried Wilhelm Leibniz was one of the first Europeans to use zero and the negatives in a systematic way in his development of calculus in the late 17th century. Calculus is used to measure rates of changes and is important in almost every branch of science, notably underpinning many key discoveries in modern physics.

Leibniz: Beaten to it by 500 years.

But Indian mathematician Bhāskara had already discovered many of Leibniz’s ideas over 500 years earlier. Bhāskara, also made major contributions to algebra, arithmetic, geometry and trigonometry. He provided many results, for example on the solutions of certain “Doiphantine” equations, that would not be rediscovered in Europe for centuries.

The Kerala school of astronomy and mathematics, founded by Madhava of Sangamagrama in the 1300s, was responsible for many firsts in mathematics, including the use of mathematical induction and some early calculus-related results. Although no systematic rules for calculus were developed by the Kerala school, its proponents first conceived of many of the results that would later be repeated in Europe including Taylor series expansions, infinitessimals and differentiation.

The leap, made in India, that transformed zero from a simple placeholder to a number in its own right indicates the mathematically enlightened culture that was flourishing on the subcontinent at a time when Europe was stuck in the dark ages. Although its reputation suffers from the Eurocentric bias, the subcontinent has a strong mathematical heritage, which it continues into the 21st century by providing key players at the forefront of every branch of mathematics.

-Christian Yates

Easy refer - Multiplication Table

Srinivasa Ramanujan

SREENIVASA RAMANUJAN

(1887–1920)

Srinivasa Ramanujan was a mathematical genius who made numerous contributions in the field, namely in number theory. The importance of his research continues to be studied and inspires mathematicians today.

Who Was Srinivasa Ramanujan?

After demonstrating an intuitive grasp of mathematics at a young age, Srinivasa Ramanujan began to develop his own theories and in 1911, he published his first paper in India. Two years later Ramanujan began a correspondence with British mathematician G. H. Hardy that resulted in a five-year-long mentorship for Ramanujan at Cambridge, where he published numerous papers on his work and received a B.S. for research. His early work focused on infinite series and integrals, which extended into the remainder of his career. After contracting tuberculosis, Ramanujan returned to India, where he died in 1920 at 32 years of age.

Early Life

Srinivasa Ramanujan was born on December 22, 1887, in Erode, India, a small village in the southern part of the country. Shortly after this birth, his family moved to Kumbakonam, where his father worked as a clerk in a cloth shop. Ramanujan attended the local grammar school and high school and early on demonstrated an affinity for mathematics.

When he was 15, he obtained an out-of-date book called A Synopsis of Elementary Results in Pure and Applied Mathematics, Ramanujan set about feverishly and obsessively studying its thousands of theorems before moving on to formulate many of his own. At the end of high school, the strength of his schoolwork was such that he obtained a scholarship to the Government College in Kumbakonam.

A Blessing and a Curse

However, Ramanujan’s greatest asset proved also to be his Achilles heel. He lost his scholarship to both the Government College and later at the University of Madras because his devotion to math caused him to let his other courses fall by the wayside. With little in the way of prospects, in 1909 he sought government unemployment benefits.

Yet despite these setbacks, Ramanujan continued to make strides in his mathematical work, and in 1911, published a 17-page paper on Bernoulli numbers in the Journal of the Indian Mathematical Society. Seeking the help of members of the society, in 1912 Ramanujan was able to secure a low-level post as a shipping clerk with the Madras Port Trust, where he was able to make a living while building a reputation for himself as a gifted mathematician.

Cambridge

Around this time, Ramanujan had become aware of the work of British mathematician G. H. Hardy — who himself had been something of a young genius — with whom he began a correspondence in 1913 and shared some of his work. After initially thinking his letters a hoax, Hardy became convinced of Ramanujan’s brilliance and was able to secure him both a research scholarship at the University of Madras as well as a grant from Cambridge

The following year, Hardy convinced Ramanujan to come study with him at Cambridge. During their subsequent five-year mentorship, Hardy provided the formal framework in which Ramanujan’s innate grasp of numbers could thrive, with Ramanujan publishing upwards of 20 papers on his own and more in collaboration with Hardy. Ramanujan was awarded a bachelor of science degree for research from Cambridge in 1916 and became a member of the Royal Society of London in 1918.

Doing the Math

"[Ramanujan] made many momentous contributions to mathematics especially number theory," states George E. Andrews, an Evan Pugh Professor of Mathematics at Pennsylvania State University. "Much of his work was done jointly with his benefactor and mentor, G. H. Hardy. Together they began the powerful "circle method" to provide an exact formula for p(n), the number of integer partitions of n. (e.g. p(5)=7 where the seven partitions are 5, 4+1, 3+2, 3+1+1, 2+2+1, 2+1+1+1, 1+1+1+1+1). The circle method has played a major role in subsequent developments in analytic number theory. Ramanujan also discovered and proved that 5 always divides p(5n+4), 7 always divides p(7n+5) and 11 always divides p(11n+6). This discovery led to extensive advances in the theory of modular forms."

Bruce C. Berndt, Professor of Mathematics at the University of Illinois at Urbana-Champaign, adds that: "the theory of modular forms is where Ramanujan's ideas have been most influential. In the last year of his life, Ramanujan devoted much of his failing energy to a new kind of function called mock theta functions. Although after many years we can prove the claims that Ramanujan made, we are far from understanding how Ramanujan thought about them, and much work needs to be done. They also have many applications. For example, they have applications to the theory of black holes in physics."

But years of hard work, a growing sense of isolation and exposure to the cold, wet English climate soon took their toll on Ramanujan and in 1917 he contracted tuberculosis. After a brief period of recovery, his health worsened and in 1919 he returned to India.

The Man Who Knew Infinity

Ramanujan died of his illness on April 26, 1920, at the age of 32. Even on his deathbed, he had been consumed by math, writing down a group of theorems that he said had come to him in a dream. These and many of his earlier theorems are so complex that the full scope of Ramanujan’s legacy has yet to be completely revealed and his work remains the focus of much mathematical research. His collected papers were published by Cambridge University Press in 1927.

Of Ramanujan's published papers — 37 in total — Berndt reveals that "a huge portion of his work was left behind in three notebooks and a 'lost' notebook. These notebooks contain approximately 4,000 claims, all without proofs. Most of these claims have now been proved, and like his published work, continue to inspire modern-day mathematics." A biography of Ramanujan titled The Man Who Knew Infinity was published in 1991, and a movie of the same name starring Dev Patel as Ramanujan and Jeremy Irons as Hardy, premiered in September 2015 at the Toronto Film Festival.

EPC 3 Exercise no.2 -Audio/ video resources for teaching Algebra

Websites....

1. https://www.educationworld.com/a_lesson/algebra-teaching-tips.shtml
2. https://www.mathtutordvd.com/
3. https://www.mathsisfun.com/algebra/index.html
4. https://www.khanacademy.org/math/algebra-home
5. https://www.intmath.com/basic-algebra/basic-algebra-intro.php:/

EPC 3 Exercise No.1- how to use computer

1. 1
   Set up your computer. If you are setting up a new desktop computer, there are a few steps you will need to go through before you can start using it. After finding a place near your desk to put the tower, you will need to connect your monitor, keyboard, and mouse, as well as plug the tower into a power source.

   • These are the only things required to be connected to the computer in order to use it. You can add more peripherals and accessories later.
   • If you are using a new laptop, you will have significantly less to set up. Plug your laptop into a power source to ensure that it is charged, and then power it on to begin.
2. 
   2
   Create a user account. If you are using the computer for the first time, you will likely be asked to create a user account when you turn it on. This account will hold all of your documents, pictures, downloaded files, and any other files that you create.

   • If your computer is in a public setting, you should create a strong password to protect your personal information. This is highly recommended, even if your computer is a home computer (To prevent someone from accessing your files).
   • How to create a new user account in Windows 7
   • How to make a new user account in Windows 8
   • How to make a new user account in OS X
3. 
   3
   Get familiar with the desktop. The desktop is the main work area of your computer, and will likely be the most visited area of your computer. Your desktop appears every time you log into your account, and contains icons and shortcuts to your most used programs and files. The desktop will look and function differently depending on which operating system you use.

   • Windows operating systems (except Windows 8) are characterized by the Start menu in the lower-left corner of the desktop. The Start menu allows you to quickly access your installed programs and settings.
   • Windows 8 has replaced the Start menu with the Start screen. It functions much the same way, but is fundamentally different in the way it displays information.
   • OS X allows you to use multiple desktops to keep things organized and under control. See this guide for details on how to take advantage of multiple desktops.
4. 
   4
   Learn mouse and keyboard basics. The mouse and keyboard are your primary means of interacting with your computer. Take some time to get familiar with how they work and how you can interact with your operating system and programs.

   • Learn how to use a mouse to navigate. Your mouse allows for pinpoint navigation and control, and is necessary for a wide variety of activities. Getting familiar with how to use the mouse will go a long way towards making you a more proficient computer user.
   • Practice some keyboard shortcuts to improve your work flow. Keyboard shortcuts are combinations of keyboard keys that perform a function in the program or operating system you are using. For example, in most programs that allow saving files, pressing Ctrl+S (⌘ Cmd+S on a Mac) will automatically save your current file.
5. 
   5
   Launch some preinstalled applications. Even if you built your computer yourself, there will be some preinstalled applications and utilities that you can use without having to install anything additional. If you are using Windows, click the Start menu and browse through your available programs. If you are using a Mac, check your Dock and Applications folder.
6. 
   6
   Install your first program. Installing software is a very common task on a computer, no matter what kind of computer you are using. The process is usually very straightforward, as most installers give clear instructions for each step.

   • Installing Microsoft Office is a good place to start if you are using a Windows computer. Having access to a word processor is invaluable, and is one of the main purposes of many people's computers. Many Windows computers come with a trial version of Office already installed.
   • Installing software on a Mac is a little bit different than installing on a Windows PC. This is mainly due to the underlying structure of the Mac operating system. Many Mac users find installing and managing programs much easier on OS X instead of Windows.

Part2

Learning Basic Computer Commands

1. 
   1
   Select files and text. You can use your mouse or keyboard shortcuts to select files on your computer and text on documents and website. Click and drag the mouse across the text you want to select, or press Ctrl+A (PC) or ⌘ Cmd+A (Mac) to select everything in your current location. Once you've selected files or text, there are several different actions you can take.
2. 
   2
   Copy and paste. Copying and pasting is one of the most common actions taken when selecting text or files. "Copying" a file or text leaves the original intact, while creating a copy on your computer's clipboard. You can then "Paste" the file or text elsewhere.

   • For PC, copy by pressing Ctrl+C and paste by pressing Ctrl+V. You can also copy and paste by right-clicking on the selection with your mouse and selecting the appropriate option from the menu.
   • For Mac, Copy by pressing ⌘ Cmd+C and paste by pressing ⌘ Cmd+V. You can also copy and paste by right-clicking on the selection with your mouse and selecting the appropriate option from the menu.
3. 
   3
   Save and open files. Many programs such as word processors, photo editors, and more allow you to create and save documents and files. When working on a computer, it is wise to save often. You never know when the power might go out, costing you hours of unsaved work. Get in the habit of saving often, and if you are making major revisions to a file it might be wise to create a new copy. You can quickly save your work in most programs that allow saving by pressing Ctrl+S (PC) or ⌘ Cmd+S (Mac).

   • If you have a lot of important files on your computer, consider setting up a backup system. This will ensure that you have at least one extra copy of all your important files should something happen to your computer. Windows and Mac OS X both have backup systems built into the operating system.
4. 
   4
   Find and sort your files. As you use your computer more and more, your personal collection of documents, media, and files may start to get a bit out of control. Take some time and organize your personal folders. You can create new folders to help create a directory of easily-accessible information.